고정 헤더 영역
상세 컨텐츠
본문
728x90
확률
표본공간[S]에 있는 각 사건과 실수 P(A)가 대응하는 집합함수
- 부분집합인 각 사건에 대해 실수값을 가지는 함수의 확률 값
- P(A)는 A의 확률[0 ≤ P(A) ≤ 1 , P(S) =1]
| 표본공간[Sample Space, S(간혹 Ω로 표기) | 모든 가능한 실험 결과들의 모임 |
| 사건[Event] | 표본공간[S]의 부분집합 |
| 원소[Element] | 나타날 수 있는 개별의 결과들을 의미 |
| 확률변수[Random Variable] | 표본공간[S]의 각 원소 S가 단 하나의 실수 X에 대응하는 함수 정의역이 표본공간 치역이 실수값[0<y<1]인 함수 |
# 집합의 연산법칙
더보기
| 교환 법칙 | A∪B=B∪A | A∩B=B∩A |
| 결합 법칙 | (A∪B)∪C=A∪(B∪C) | (A∩B)∩C=A∩(B∩C) |
| 분배 법칙 | A∩(B∪C)=(A∩B)∪(A∩C) | A∪(B∩C)=(A∪B)∩(A∪C) |
| 드모르간[De Morgan] 법칙 | (A∪B)c=Ac∩Bc | (A∩B)c=Ac∪Bc |
확률의 성질
① P(A) = 1-P(Ac)
더보기
| 1=P(S)=P(A∪Ac)=P(A)+P(Ac) → A와 Ac는 배반사건[A∩Ac=ø]이므로 ∴ P(A)=1-P(Ac) |
② P(ø) = 0
더보기
| 1=P(S)=P(S∪ø)=P(S)+P(ø) → S와 ø는 배반사건[S∩ø=ø]이므로 ∴ P(ø)=1-P(S)=0 |
③ A⊂B이면 P(A)≤P(B)
더보기
| B=A∪(B∩Ac) , A∩(B∩Ac)=ø이므로 ∴ P(A)≤P(B) = P(A∪(B∩Ac) = P(A) + P(B∩Ac) |
④ 0≤P(A)≤1
더보기
| ø⊂A⊂S에서 정리③에 의해 P(ø)⊂P(A)⊂P(S) ∴ 0≤P(A)≤1 |
⑤ P(A∪B)=P(A)+P(B)-P(A∩B) → 확률의 덧셈정리
더보기
| P(A∪B) = P(A∪(B∩Ac)) = P(A) + P(B∩Ac) → A와 B∩Ac가 배반사건[A∩(B∩Ac)] P(B) = P[(A∩B)∪(B∩Ac)] = P(A∩B) + P(B∩Ac) → A∩B와 B∩Ac가 배반사건[P(A∩B)∩P(B∩Ac)=ø] ∴ P(A∪B) = P(A) + P(B) - P(A∩B) |
⑥ P(A∪BUC)=P(A)+P(B)+P(C)-P(A∩B)-P(A∩C)-P(B∩C)+P(A∩B∩C)
확률변수의 종류
확률변수는 0이 아닌 확률을 갖는 실수값의 형태에 따라 이산형확률변수와 연속형 확률변수로 구분된다.
| 확률 변수의 종류 | 이산형 확률변수 [Discrete Random Variable] |
연속형 확률변수 [Continuous Random Variable] |
| 정 의 | 확률 변수 X가 유한 집합이거나 자연수의 부분집합과 일대일 대응일 때의 확률변수 | 임의의 구간을 설정해도 구간 내의 값을 측정할 수 없는 확률변수 |
| 확률분포함수 |
확률질량함수 | 확률밀도함수 |
| 확률변수X의 기대값 | E(X) = ∑xif(xi) | E(X) = ∫xf(x)dx |
| 확률변수X의 k차 적률 | E(Xk) = ∑xikf(xi) | E(Xk) = ∫xkf(x)dx |
| 확률변수[X]의 k차 중심적률 | E[(X-μ)k] = ∑(xi-μ)kf(xi) | E[(X-μ)k] = ∫(x-μ)kf(x) |
# 모분산[Population Variance, σ2]
더보기
σ2 = E[(X-μ)2] = E[(X2-2μX+μ2)] = E(X2)-2μE(X)+μ2 = E(X2)-μ2
즉, 모분산은 [2차적률-(1차적률)2]으로 해석 가능
순열[Permutation]과 조합[Combination]
| 순열[Permutation] | 순서고려 |
| 조합[Combination] | 순서고려 X |
복원추출 & 비복원 추출
| 복원추출 | 다음 표본 추출 전 추출된 표본이 복원되는 추출 방법 |
| 비복원추출 | 추출된 표본이 복원되지 않는 추출 방법 |
# 초기하 분포[Hypergeometric Distribution]
더보기
크기가 유한한 모집단으로부터 비복원 추출 시 나타나는 확률분포
ex> n = n1 + n2일때, r개 추출 |
ex> 100개[양품80, 불량20개] 중 5개를 추출할 때, 불량품이 0개인 확률은? |
이항정리
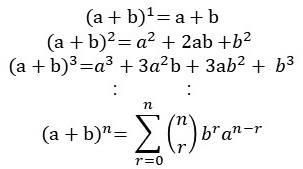
이항정리의 일반화[다항정리]
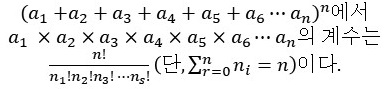
파스칼 정리

- n개 중 r개를 뽑는 확률은 n-1개 중[1개를 미리 뽑았을 때] r개에 포함이 됨 경우와 안된 경우의 합
조건부확률
사건 B가 주어졌을 때 사건 A가 일어날 확률 [P(A|B)]

확률의 곱셈법칙

전확률의 정리

베이즈 정리

독립사건
사건 A와 B가 서로 독립인 필요충분조건은 P(A∩B)=P(A)XP(B)이다.
- P(A|B) = P(A)
- 사건 A와 B가 독립이면 A와 Bc, Ac와 B, Ac와 Bc도 모두 독립
728x90
'자격증 > ADsP' 카테고리의 다른 글
| [개미의 걸음 ADsP 3과목] 통계분석의 이해 (0) | 2021.02.17 |
|---|---|
| [개미의 걸음 ADsP 3과목] 확률분포① 이산형 확률 분포 (0) | 2021.02.15 |
| [개미의 걸음 ADsP 3과목] EDA & 결측치 및 이상치 처리 (0) | 2021.02.13 |
| [개미의 걸음 ADsP 3과목] 데이터 가공(변수의 중요도 및 구간화) (0) | 2021.02.12 |
| [개미의 걸음 ADsP 3과목] 데이터 마트 ① reshape 패키지 (0) | 2021.02.11 |





댓글 영역